Оглавление статьи
Фрактальная теория Бенуа Мандельброта изменила наше понимание природы, экономики и даже финансовых рынков. Эта теория, основанная на изучении сложных геометрических структур, раскрывает, как хаотические процессы могут быть упорядоченными. Более того, она нашла применение в самых разных областях — от физики до криптотрейдинга. В этой статье мы разберем, что такое фракталы, как Мандельброт разработал свою теорию, почему она актуальна сегодня, и как ее используют в торговле криптовалютами.
Что такое фракталы и почему они важны?
Фракталы — это геометрические фигуры, которые повторяют свои узоры на разных масштабах. Например, если рассмотреть лист папоротника, его структура повторяется в меньших масштабах.

Именно эту идею Бенуа Мандельброт систематизировал в своей теории. Он показал, что фрактальные структуры встречаются повсюду: в облаках, береговых линиях, ветвях деревьев и даже в движении цен на финансовых рынках.
Фракталы отличаются самоподобностью. Это значит, что их части выглядят как целое, независимо от масштаба. Более того, фракталы позволяют описывать сложные системы, которые кажутся хаотичными. Например, турбулентность в жидкостях или колебания на фондовом рынке. Именно поэтому теория Мандельброта так важна. Она помогает находить порядок в кажущемся хаосе.
Мандельброт ввел термин «фрактал» в 1975 году. Он происходит от латинского слова fractus, что означает «ломаный» или «разделенный». В отличие от классической геометрии, фракталы не имеют гладких линий. Вместо этого они состоят из неровных, ломаных форм. Это делает их уникальными и универсальными для описания природных явлений.
Кто такой Бенуа Мандельброт?
Бенуа Мандельброт — математик, родившийся в 1924 году в Польше. Его семья переехала во Францию, чтобы избежать преследований во время Второй мировой войны. Уже в молодости он проявил талант к математике. Однако Мандельброт не ограничивался одной областью. Он работал в IBM, исследовал экономику, физику и даже лингвистику.
Его главный вклад — развитие фрактальной геометрии. В 1982 году он опубликовал книгу «Фрактальная геометрия природы», которая стала классикой. В этой книге Мандельброт показал, как фракталы описывают сложные системы. Более того, он сделал математику доступной для широкой аудитории. Его идеи вдохновили ученых, инженеров и даже трейдеров.
Мандельброт также разработал знаменитое множество Мандельброта. Это математический объект, который стал символом фрактальной теории. Его визуализация поражает воображение: бесконечные узоры, которые раскрываются при увеличении. Именно это множество стало иконой фрактальной геометрии.
Фрактал Бенуа Мандельброта или как его еще называют: множество Мандельброта
Это фрактал, представляющий множество точек на комплексной плоскости, для которых определённая рекуррентная последовательность остаётся ограниченной. Он известен своей бесконечной сложностью и самоподобием при увеличении.
📹 Видео Фрактала (множества) Бенуа Мандельброта
Если вы хотите исследовать множество Мандельброта самостоятельно, вы можете воспользоваться интерактивным онлайн-навигатором, например, на сайте mandelbrot.site, который позволяет масштабировать и сохранять изображения в высоком разрешении.
На сайте можно менять цветовую палитру и параметры множества получая живописные картинки наподобии этой:

Фрактал Бенуа Мандельброта (или множество Мандельброта) строится с помощью простой, но мощной рекуррентной формулы в комплексной плоскости.
🔷 Формула множества Мандельброта:
zn+1=zn2+cz_{n+1} = z_n^2 + c
где:
- z0=0z_0 = 0
- c∈Cc \in \mathbb{C} — произвольное комплексное число (каждая точка плоскости)
- последовательность {zn}\{z_n\} проверяется на ограниченность (не стремится к бесконечности)
🔍 Условие принадлежности к множеству:
Число cc принадлежит множеству Мандельброта, если при повторном применении формулы zn+1=zn2+cz_{n+1} = z_n^2 + c начиная с z0=0z_0 = 0, модуль ∣zn∣|z_n| остаётся ограниченным (не уходит в бесконечность) при n→∞n \to \infty.
💡 На практике:
- Если после определённого количества итераций (например, 1000) модуль ∣zn∣>2|z_n| > 2, то точка cc не принадлежит множеству.
- Если не превышает — точка считается принадлежащей фракталу.
Основы фрактальной теории
Фрактальная теория изучает объекты, которые обладают самоподобностью и нерегулярностью. Например, береговая линия выглядит изломанной, но при увеличении ее части повторяют структуру целого. Мандельброт показал, что такие объекты имеют дробную размерность. В отличие от обычных фигур (линия — 1, квадрат — 2, куб — 3), фракталы имеют нецелую размерность, например, 1.7 или 2.3.
Кроме того, фракталы описывают системы с высокой степенью сложности. Они не подчиняются простым законам классической физики. Например, движение цен на рынке кажется случайным. Однако фрактальная теория показывает, что в этом хаосе есть скрытые закономерности.
Мандельброт также изучал распределение данных. Он обнаружил, что многие природные и экономические процессы следуют «тяжело-хвостатым» распределениям. Это значит, что экстремальные события (например, резкие скачки цен) происходят чаще, чем предсказывает нормальное распределение. Именно поэтому его теория так важна для анализа рисков.
Применение фракталов в природе
Фракталы встречаются повсюду в окружающем мире. Например, горные хребты имеют фрактальную структуру. Их вершины и склоны повторяются в разных масштабах. То же самое касается облаков, молний и даже кровеносных сосудов в организме человека.
Более того, фракталы помогают моделировать сложные процессы. Например, в метеорологии они используются для прогнозирования погоды. Фрактальные модели лучше описывают турбулентность в атмосфере. Кроме того, в биологии фракталы применяются для изучения роста растений и структуры ДНК.
Интересно, что фракталы нашли применение и в искусстве. Художники используют фрактальные алгоритмы для создания сложных узоров. Например, компьютерная графика в фильмах и играх часто основана на фрактальных структурах. Это делает изображения более реалистичными.
Фракталы в экономике и финансах
Мандельброт применил свою теорию к экономике. Он заметил, что финансовые рынки ведут себя не так, как предсказывает классическая экономическая теория. Например, стандартные модели предполагают, что цены изменяются плавно. Однако Мандельброт показал, что рынки демонстрируют резкие скачки и фрактальную структуру.
Его идеи изменили подход к анализу рисков. Традиционные модели, такие как модель Блэка-Шоулза, недооценивают вероятность экстремальных событий. В результате трейдеры и инвесторы часто оказывались неподготовленными к кризисам. Фрактальная теория помогает лучше прогнозировать такие события.
Кроме того, Мандельброт изучал волатильность рынков. Он показал, что колебания цен имеют фрактальный характер. Это значит, что графики цен выглядят одинаково на разных временных масштабах. Например, дневной график может быть похож на недельный или часовой. Эта самоподобность стала ключом к новым методам анализа.
Связь фракталов Мандельброта с волнами Эллиотта в трейдинге
Теория волн Эллиотта, разработанная Ральфом Нельсоном Эллиоттом в 1930-х годах, описывает поведение цен на финансовых рынках как фрактальную структуру, состоящую из повторяющихся паттернов, которые подчиняются определённой логике и психологии участников рынка.
Что такое волны Эллиотта?
Согласно Эллиотту, рыночное движение состоит из двух основных фаз:
- Импульсные волны (1-2-3-4-5) — движение по тренду
- Коррекционные волны (A–B–C) — движение против тренда
Эти волны образуют 5-3 структуру, которая повторяется на всех таймфреймах, от минутных графиков до многолетних. Каждая волна в свою очередь делится на подволны, образуя фрактал.
Волны Эллиотта как фрактал
Как и множество Мандельброта, волны Эллиотта обладают самоподобием:
- Внутри каждой волны можно найти более мелкие волны с такой же структурой
- Это делает модель фрактальной по своей сути — как математические фракталы, только в контексте поведения толпы на рынке
Общая идея
И множество Мандельброта, и волны Эллиотта опираются на:
- Итерации и повторение паттернов
- Самоподобие и масштабируемость
- Нелинейную динамику и чувствительность к начальному состоянию
Таким образом, теория Эллиотта — это практическое применение фрактальных принципов в трейдинге.
Фракталы в трейдинге и криптотрейдинге. Стратегия на основе индикатора Билла Вильямса
Криптовалютные рынки — идеальное поле для применения фрактальной теории. Цены на биткоин, эфириум и другие криптовалюты часто демонстрируют высокую волатильность. Более того, их движение кажется хаотичным. Однако фрактальная теория помогает находить закономерности.
Почему фракталы важны для криптотрейдинга?
Криптовалютные рынки имеют несколько особенностей. Во-первых, они работают 24/7, что делает их более динамичными. Во-вторых, они подвержены резким скачкам цен. Например, в 2021 году биткоин вырос с $29,000 до $69,000, а затем упал до $40,000 за несколько месяцев. Такие движения сложно предсказать с помощью традиционных моделей.
Фрактальная теория предлагает другой подход. Она позволяет трейдерам анализировать графики цен на разных временных масштабах. Например, трейдер может заметить повторяющиеся паттерны на часовом, дневном или недельном графике. Это помогает прогнозировать точки разворота или тренды.
Как использовать фракталы в торговле?
В криптотрейдинге фракталы часто применяются в техническом анализе. Например, индикатор «Фрактал» Билла Вильямса помогает находить ключевые уровни поддержки и сопротивления. Этот индикатор основан на идее Мандельброта о самоподобности. Он выявляет локальные максимумы и минимумы на графике.
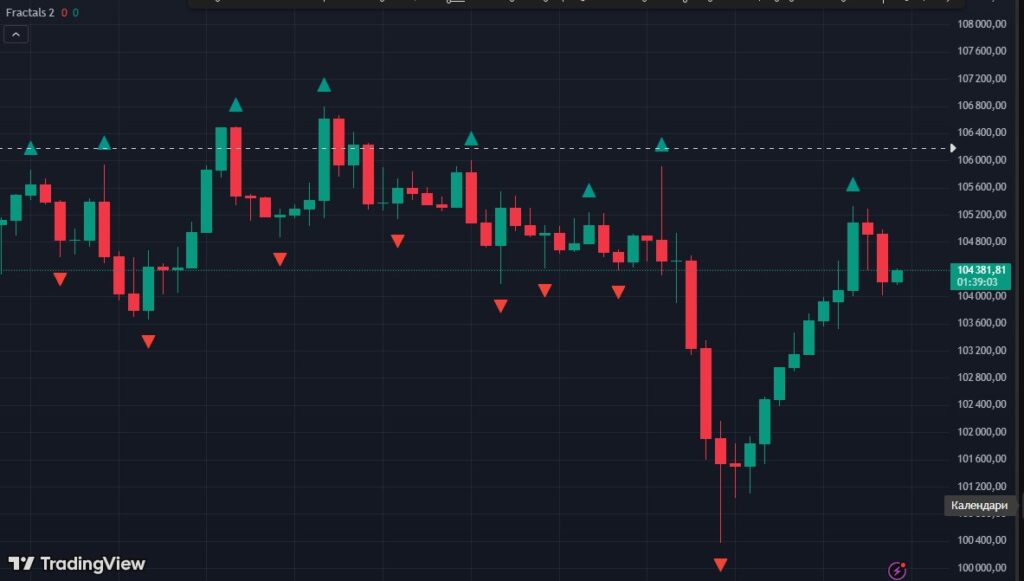
Вот как работает индикатор:
- Фрактал формируется, когда центральная свеча (или бар) окружена двумя свечами с более низкими максимумами (для медвежьего фрактала) или более высокими минимумами (для бычьего фрактала).
- Эти точки указывают на потенциальные уровни разворота.
- Трейдеры используют фракталы для установки стоп-лоссов или определения точек входа.
Например, если на дневном графике биткоина формируется бычий фрактал, это может сигнализировать о начале восходящего тренда. Трейдер может открыть длинную позицию, установив стоп-лосс ниже фрактального уровня.
Преимущества и ограничения
Фракталы дают трейдерам несколько преимуществ:
- Универсальность. Фрактальные паттерны работают на всех таймфреймах.
- Простота. Индикатор легко интегрируется в торговые платформы, такие как TradingView.
- Надежность. Фракталы помогают находить ключевые уровни даже в условиях высокой волатильности.
Однако есть и ограничения. Во-первых, фракталы запаздывают, так как формируются после нескольких свечей. Во-вторых, они не всегда точны в условиях сильного тренда. Поэтому трейдерам стоит комбинировать фракталы с другими индикаторами, такими как RSI или скользящие средние.
Практическое применение в криптотрейдинге. Стратегия.
Для успешного использования фракталов в криптотрейдинге следуйте этим шагам:
- Выберите таймфрейм. Для краткосрочной торговли подойдет 1-часовой график, для долгосрочной — дневной.
- Найдите фракталы. Используйте индикатор Вильямса или анализируйте графики вручную.
- Подтвердите сигнал. Проверьте, совпадает ли фрактал с другими индикаторами, например, уровнями Фибоначчи.
- Управляйте рисками. Устанавливайте стоп-лоссы и не рискуйте более 1-2% депозита на сделку.
Например, трейдер замечает бычий фрактал на 4-часовом графике эфириума. Цена находится около уровня поддержки $2,500. Он открывает длинную позицию, устанавливая стоп-лосс на $2,450. Если цена вырастает до $2,700, он фиксирует прибыль.
Современное значение фрактальной теории
Сегодня фрактальная теория остается актуальной. Она применяется в самых разных областях: от компьютерной графики до анализа больших данных. Более того, развитие технологий сделало фракталы еще более востребованными. Например, машинное обучение использует фрактальные алгоритмы для обработки сложных данных.
В финансах фрактальная теория помогает лучше понимать риски. Она показывает, что экстремальные события не так редки, как кажется. Это особенно важно в эпоху криптовалют, где волатильность может достигать сотен процентов.
Кроме того, фракталы вдохновляют новые исследования. Ученые изучают их применение в квантовой физике, биоинформатике и даже социологии. Например, фрактальные модели помогают анализировать поведение толпы или распространение информации в соцсетях.
Критика и ограничения фрактальной теории
Несмотря на популярность, теория Мандельброта имеет критиков. Некоторые ученые считают, что фракталы слишком абстрактны. Например, в экономике сложно точно измерить фрактальную размерность. Кроме того, не все системы подчиняются фрактальным законам.
В криптотрейдинге фракталы также не являются универсальным инструментом. Они работают лучше в сочетании с другими методами. Более того, высокая волатильность криптовалют может приводить к ложным сигналам. Поэтому трейдерам важно быть осторожными.
Заключение
Фрактальная теория Бенуа Мандельброта — это мощный инструмент для понимания сложных систем. Она раскрывает скрытые закономерности в природе, экономике и финансах. Более того, она нашла практическое применение в трейдинге. Фракталы помогают трейдерам находить ключевые уровни и прогнозировать движение цен.
Однако теория требует осторожного подхода. Она не дает 100% точных прогнозов, особенно в условиях высокой волатильности. Тем не менее, идеи Мандельброта продолжают вдохновлять ученых, инженеров и трейдеров. Они показывают, что даже в хаосе можно найти порядок.
Если вы хотите глубже изучить фракталы, начните с книги Мандельброта «Фрактальная геометрия природы». Для трейдеров полезно освоить индикатор фракталов на платформах вроде TradingView. В любом случае, теория Мандельброта остается мостом между математикой, природой и финансами.

